Push-Pull Transformers

What I intend to show is that the effective impedance (also called the composite impedance) seen by the pair of tubes in a push pull amplifier is 1/4 the end to end plate impedance of the transformer. From this we'll see that the load line seen by each tube in a pair of push-pull tubes depends on whether or not the tubes are biased class A or class B:

1. The volts per turn on a leg of a transformer are constant. This rule is independent of the direction the current is flowing with respect to the dot.

4.1 The volts / turn is set by the voltage on the drive winding after IR drop (Current Winding 1 * Winding 1's resistance) is subtracted from the drive winding's voltage.

2.3a I1 = I2 * N2 / N1 + V1 /{ j * 2 * pi * F * Lpri } + [ Core loss watts / V1 ]
The "j" is to remind us that this is a vector addition of currents. Remember, the core loss will be in phase with a reflected "resistive" load current. In this next equation, rms currents and voltages are used.

I1 = sqrt [ ( I2 * N2 / N1 + [Core loss watts / V1] )^2 + ( V1 /{ 2 * pi * F * Lpri} )^2 ]

The Mathematical Push-Pull Impedance Example
Last Update 30-Dec-04

If the secondary turns are N2 and the full primary turns are 2 * N1, the impedance ratio from the full primary to the secondary is (2 * N1 / N2 )^2 or 4 * (N1/N2)^2. The impedance ratio for one half the primary is just (N1/N2)^2. The impedance of 1/2 the primary winding is 1/4 the impedance of the end to end primary.

If the output load is 8 ohms and N1/N2 is 25, then 8 ohms * (N1 / N2)^2 is 5000 ohms. The impedance across the entire primary will be four times the impedance across half the primary. Four times the half primary impedance is 20 kohm. This transformer would be rated at an impedance ratio of 20k:8.

If the tubes are biased into class A, they will share the load when driving the primary. When these two "parallel" tubes share a load line (a composite load line), the pair of tubes together see an impedance of (N1 / N2)^2. However, because there are two tubes sharing the load, the load line for each tube is twice the composite load line or 2 * (N1 / N2)^2.

With 400V across the entire primary, 20 mA will be flowing through the primary for an input power of 8 watts.
With 2 * N1 / N2 = 2 * 25, the ideal secondary voltage will be 400V / (2 * 25) = 8V
The ideal secondary current is 20 mA * (2 * 25) = 1 amp
The output power is 8 V * 1 A = 8W.
One tube will swing half the voltage (200V), but swings only 20 mA. 200V/ 20 mA is 10 kohm. 10 kohm is 1/2 the full primary winding impedance.

If tube 1 (P1) is removed, the impedance seen by tube 2 on primary 2 (P2) is (N1 / N2)^2. This is 1/4, not 1/2, the end to end primary impedance. This makes sense, the output power to the load hasn't changed, the P1 winding isn't contributing to supporting the output load and P2 must support the full output load.

If P1 is removed and P2 is to drive 200V across N1, P2 must now conduct 40 mA not 20 mA to deliver the same power to the load. This is to meet the amp-turns requirement of the output winding N2 reflected back to the primary with a 25:1 turns ratio.
I(P2) = 1A * 1 / 25 = 0.040A = 40 mA.
The impedance seen by the tube 200V/ 40 mA which is 5000 ohms.

The same is true for P1 when tube 2 is removed. P1 sees (N1 / N2)^2 or 1/4 the end to end primary impedance. This is the class B bias case. In class B only one tube is active at a time.

If this is confusing, keep reading. I've got pictures below to help out.

Moving Windings Around
Last Update 26-Sep-04

The purpose of this exercise is to get us use to how the current, voltage and impedance behaves as the windings are move around. In of these examples 1 through 4, there is 8 watts going into the transformer.

Starting with picture 1, we have a 400 V source consisting of two series 200V sources. This 400 V source is providing 20 mA into an effective load of 20 kohm. Notice that at the center tap (B C), there is zero total current flowing. The wire shown between the voltage source and the transformer does not have to be there.

In picture 2, we split the common center tap into two floating windings. The total impedance is still 20 kohm and each 200V source is driving 10 kohm ( 200V/ 20 mA)

In picture 3 the two sources are shown floating in parallel. Each source still sees a load of 10 kohm (200V / 20 mA), however, the composite load is 5 kohm (200V / 40 mA)

In picture 4, one source is removed and the composite load is kept the same. This one source sees a load of 5 kohm (200V / 40 mA). The single 200V source sees a lower impedance load because the other 200V source is not helping support the composite load of 5 kohm.

The composite load in picture 4 is 1/4 the load in picture 1. This is because the load in picture 4 has half the turns as the load in picture 1. This should be no surprise because we knowing the rule on reflected impedances:

Z1 / Z2 = (N1 / N2 )^2,
Z1 / Z2 = (1 / 2)^2 or 1/4.

Picture 4 is equivalent to a class B push pull amplifier where only one source (one tube) must support the entire load. In a class B amplifier, the load line on the active tube (the voltage) source is 1/4 the plate to plate impedance shown in picture 1.

Picture 3 is equivalent to a class A push pull amplifier. The composite load is the same as picture 4, but each tube only has to supply 1/2 the current for the same voltage swing. So each individual tube in a class A push-pull amplifier sees a load of 1/2 the plate to plate impedance (20 kohm) or twice the composite impedance (5 kohm). Remember, the load line on each individual tube is twice the impedance of composite load line because both tubes are supporting the load.

Lets look at the primary of an ideal transformer driven by an ideal tube at biased class A both at when the output is at idle and when swinging full output power:

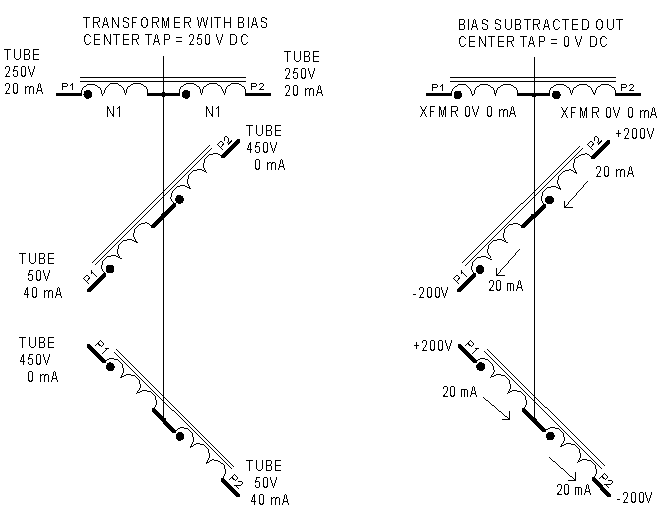
Plate 1 (P1) sees a peak swing of 200V and 20 mA for an impedance of 200V / 20 mA = 10 kohm
Plate 2 (P2) sees a peak swing of 200V and 20 mA for an impedance of 200V / 20 mA = 10 kohm
From plate 1 to plate 2 we see a peak swing of 400V and 20 mA for an impedance of 400V / 20 mA = 20 kohm
On a Push-Pull transformer driven by tube biased to class A, each individual tube sees 1/2 the full primary impedance as its load line.

Push-Pull to Single Ended Graphical Example.
Last Update 26-Sep-04

The load sharing may become more apparent if we convert the push-pull to parallel single ended (push-push).

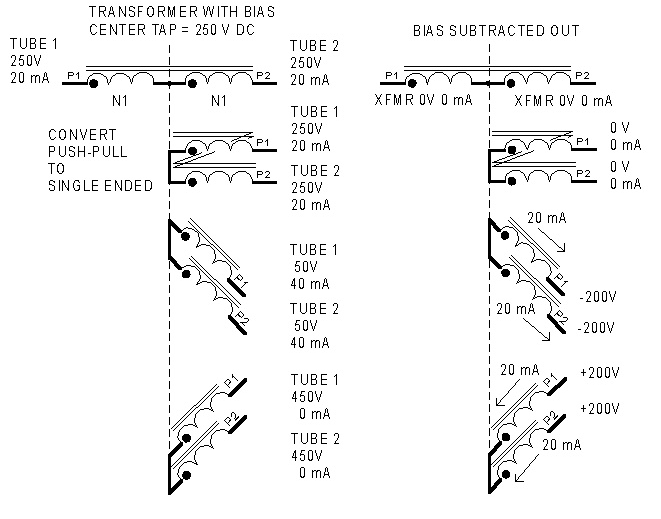
The two tubes in parallel swing 200V peak and 40 mA peak total.

Z composite load = 200 V / 40 mA = 5 kohm

Each individual tube is swinging 200V peak and 20 mA peak.

Z each tube = 200 V / 20 mA = 10 kohm

Again if we pull tube 1, tube 2 must support the full (composite) load of 5 kohm.

Summary Class B Push-Pull Operation
Last Update 26-Sep-04

In class B operation, only one tube is supporting the load across N1. So the impedance ratio seen by the tube is ( N1 / N2 )^2. This is 1/4 the full primary impedance. Class B sees 1/4 the end to end transformer impedance because only half the turns on the transformer are driven. Class B has half the load impedance as class A because only 1 tube is active.

I've noticed several posts on the internet where voltage and current are added incorrectly. I have a water analogy that may help people keep this straight.

If two hoses are tied to the same inlet, the pressure at the inlet is the same for both hoses. If these two hoses are also tied at the outlet, the pressure is the same on the outlet side. If the hoses are the same diameter and length, you get twice the gallons / second through two hoses with the same pressure drop as one hose.